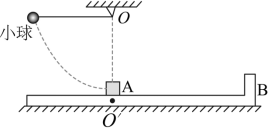
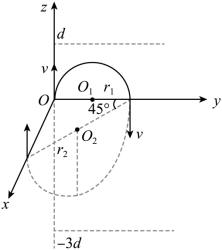
如图所示, “L” 型平板 B 静置在地面上,小物块 A 处于平板 B 上的 点,
点左侧粗糙,右侧光滑。用不可伸长的轻绳将质量为 M 的小球悬挂在
点正上方的 O 点,轻绳处于水平拉直状态。将小球由静止释放,下摆至最低点与小物块 A 发生碰撞,碰后小球速度方向与碰前方向相同,开始做简谐运动(要求摆角小于
), A 以速度
沿平板滑动直至与 B 右侧挡板发生弹性碰撞。一段时间后, A 返回到 O 点的正下方时,相对于地面的速度减为零,此时小球恰好第一次上升到最高点。已知 A 的质量
, B 的质量
, A 与 B 的动摩擦因数
, B 与地面间的动摩擦因数
,取重力加速度
。整个过程中 A 始终在 B 上,所有碰撞时间忽略不计,不计空气阻力,求:
( 1 ) A 与 B 的挡板碰撞后,二者的速度大小 与
;
( 2 ) B 光滑部分的长度 d ;
( 3 )运动过程中 A 对 B 的摩擦力所做的功 ;
( 4 )实现上述运动过程, 的取值范围(结果用
表示)。
( 1 ) ,
;( 2 )
;( 3 )
;( 4 )
【详解】( 1 )设水平向右为正方向,因为 点右侧光滑,由题意可知 A 与 B 发生弹性碰撞,故碰撞过程根据动量守恒和能量守恒有
代入数据联立解得
,(方向水平向左)
,(方向水平向右)
即 A 和 B 速度的大小分别为 ,
。
( 2 )如图所示为 A 与 B 挡板碰撞后到运动至 O 点正下方的运动示意图
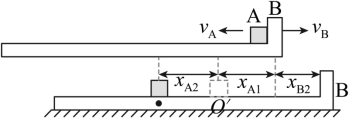
A 回到 前, A 在 B 上匀速直线运动的时间设为
。 A 的位移大小
对平板 B ,由牛顿第二定律得
对平板 B ,由运动学公式有
由几何关系
①
A 从 回到 O 点正下方设时间为
, A 在 B 上做匀减速直线运动,设 A 的加速度大小为
,由牛顿第二定律得
解得
A 返回到 O 点的正下方时,相对于地面的速度减为零,则
时间内 A 相对于地面的位移大小
由几何关系
②
联立解得
或
,
由 ①② 可得
与
等大
分析可知, A 回到 O 点正下方时 B 未减速为 0 ,故
舍去。综上解得
( 3 )在 A 刚开始减速时, B 物体的速度为
在 A 减速过程中,对 B 分析根据牛顿运动定律可知
解得
B 物体停下来的时间为 t 3 ,则有
解得
可知在 A 减速过程中 B 先停下来了,此过程中 B 的位移为
所以 A 对 B 的摩擦力所做的功为
( 4 )小球和 A 碰撞后 A 做匀速直线运动再和 B 相碰,此过程有
由题意可知 A 返回到 O 点的正下方时,小球恰好第一次上升到最高点,设小球做简谐振动的周期为 T ,摆长为 L ,则有
由单摆周期公式 解得,小球到悬挂点 O 点的距离
小球下滑过程根据动能定理有
当碰后小球摆角恰为 5° 时,有
解得
,
小球与 A 碰撞过程根据动量守恒定律有
小球与 A 碰后小球速度方向与碰前方向相同,开始做简谐运动(要求摆角小于 ),则要求
故要实现这个过程的范围为
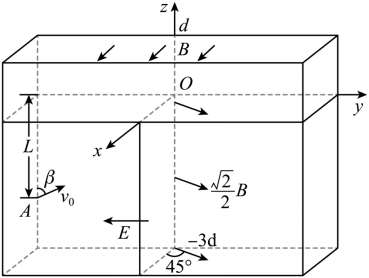
中国 “ 人造太阳 ” 在核聚变实验方面取得新突破,该装置中用电磁场约束和加速高能离子,其部分电磁场简化模型如图所示,在三维坐标系 中,
空间内充满匀强磁场 I ,磁感应强度大小为 B ,方向沿 x 轴正方向;
,
的空间内充满匀强磁场 II ,磁感应强度大小为
,方向平行于
平面,与 x 轴正方向夹角为
;
,
的空间内充满沿 y 轴负方向的匀强电场。质量为 m 、带电量为
的离子甲,从
平面第三象限内距
轴为
的点
以一定速度出射,速度方向与
轴正方向夹角为
,在
平面内运动一段时间后,经坐标原点
沿
轴正方向进入磁场 I 。不计离子重力。
( 1 )当离子甲从 点出射速度为
时,求电场强度的大小
;
( 2 )若使离子甲进入磁场后始终在磁场中运动,求进入磁场时的最大速度 ;
( 3 )离子甲以 的速度从
点沿
轴正方向第一次穿过
面进入磁场 I ,求第四次穿过
平面的位置坐标(用 d 表示);
( 4 )当离子甲以 的速度从
点进入磁场 I 时,质量为
、带电量为
的离子乙,也从
点沿
轴正方向以相同的动能同时进入磁场 I ,求两离子进入磁场后,到达它们运动轨迹第一个交点的时间差
(忽略离子间相互作用)。
( 1 ) ;( 2 )
;( 3 )( d , d ,
);( 4 )
【详解】( 1 )如图所示
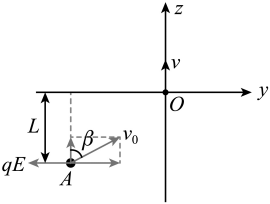
将离子甲从 点出射速度为
分解到沿
轴方向和
轴方向,离子受到的电场力沿
轴负方向,可知离子沿
轴方向做匀速直线运动,沿
轴方向做匀减速直线运动,从
到
的过程,有
联立解得
( 2 )离子从坐标原点 沿
轴正方向进入磁场 I 中,在磁场 I 中做匀速圆周运动,经过磁场 I 偏转后从
轴进入磁场 II 中,继续做匀速圆周运动,如图所示
由洛伦兹力提供向心力可得
,
可得
为了使离子在磁场中运动,则离子磁场 I 运动时,不能从磁场 I 上方穿出。在磁场 II 运动时,不能 xOz 平面穿出,则离子在磁场用运动的轨迹半径需满足
,
联立可得
要使离子甲进入磁场后始终在磁场中运动,进入磁场时的最大速度为 ;
( 3 )离子甲以 的速度从
点沿 z 轴正方向第一次穿过
面进入磁场 I ,离子在磁场 I 中的轨迹半径为
离子在磁场 II 中的轨迹半径为
离子从 点第一次穿过到第四次穿过
平面的运动情景,如图所示
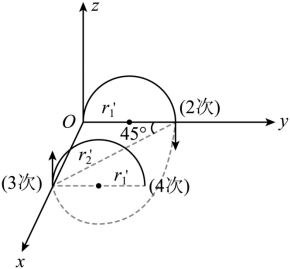
离子第四次穿过 平面的
坐标为
离子第四次穿过 平面的
坐标为
故离子第四次穿过 平面的位置坐标为( d , d ,
)。
( 4 )设离子乙的速度为 ,根据离子甲、乙动能相同,可得
可得
离子甲、离子乙在磁场 I 中的轨迹半径分别为
,
离子甲、离子乙在磁场 II 中的轨迹半径分别为
,
根据几何关系可知离子甲、乙运动轨迹第一个交点在离子乙第一次穿过 x 轴的位置,如图所示
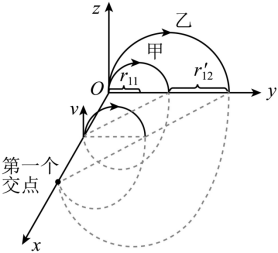
从 点进入磁场到第一个交点的过程,有
可得离子甲、乙到达它们运动轨迹第一个交点的时间差为
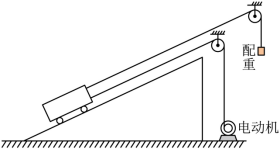
某粮库使用额定电压 ,内阻
的电动机运粮。如图所示,配重和电动机连接小车的缆绳均平行于斜坡,装满粮食的小车以速度
沿斜坡匀速上行,此时电流
。关闭电动机后,小车又沿斜坡上行路程 L 到达卸粮点时,速度恰好为零。卸粮后,给小车一个向下的初速度,小车沿斜坡刚好匀速下行。已知小车质量
,车上粮食质量
,配重质量
,取重力加速度
,小车运动时受到的摩擦阻力与车及车上粮食总重力成正比,比例系数为 k ,配重始终未接触地面,不计电动机自身机械摩擦损耗及缆绳质量。求:
( 1 )比例系数 k 值;
( 2 )上行路程 L 值。
( 1 ) ;( 2 )
【详解】( 1 )设电动机的牵引绳张力为 ,电动机连接小车的缆绳匀速上行,由能量守恒定律有
解得
小车和配重一起匀速,设绳的张力为 ,对配重有
设斜面倾角为 ,对小车匀速有
而卸粮后给小车一个向下的初速度,小车沿斜坡刚好匀速下行,有
联立各式解得
,
( 2 )关闭发动机后小车和配重一起做匀减速直线运动,设加速度为 ,对系统由牛顿第二定律有
可得
由运动学公式可知
解得
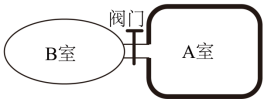
某些鱼类通过调节体内鱼鳔的体积实现浮沉。如图所示,鱼鳔结构可简化为通过阀门相连的 A 、 B 两个密闭气室, A 室壁厚、可认为体积恒定, B 室壁簿,体积可变;两室内气体视为理想气体,可通过阀门进行交换。质量为 M 的鱼静止在水面下 H 处。 B 室内气体体积为 V ,质量为 m ;设 B 室内气体压强与鱼体外压强相等、鱼体积的变化与 B 室气体体积的变化相等,鱼的质量不变,鱼鳔内气体温度不变。水的密度为 ρ ,重力加速度为 g 。大气压强为 p 0 ,求:
( 1 )鱼通过增加 B 室体积获得大小为 a 的加速度、需从 A 室充入 B 室的气体质量 D m ;
( 2 )鱼静止于水面下 H 1 处时, B 室内气体质量 m 1 。
( 1 ) ;( 2 )
【详解】( 1 )由题知开始时鱼静止在 H 处,设此时鱼的体积为 ,有
且此时 B 室内气体体积为 V ,质量为 m ,则
鱼通过增加 B 室体积获得大小为 a 的加速度,则有
联立解得需从 A 室充入 B 室的气体质量
( 2 ) B 室内气体压强与鱼体外压强相等,则鱼静止在 H 处和水面下 H 1 处时, B 室内的压强分别为
,
由于鱼静止时,浮力等于重力,则鱼的体积不变,由于题可知,鱼体积的变化与 B 室气体体积的变化相等,则鱼在水下静止时, B 室内气体体积不变,由题知开始时鱼静止在 H 处时, B 室内气体体积为 V ,质量为 m ,由于鱼鳔内气体温度不变,若 ,则在 H 处时, B 室内气体需要增加,设吸入的气体体积为 Δ V ,根据玻意耳定律有
则此时 B 室内气体质量
若 ,则在 H 处时, B 室内气体需要减少,设释放的气体体积为 Δ V ,根据玻意耳定律有
则此时 B 室内气体质量
某同学利用实验室现有器材,设计了一个测量电阻阻值的实验。实验器材:
干电池 E (电动势 1.5V ,内阻未知);
电流表 A 1 (量程 10mA ,内阻为 90Ω );
电流表 A 2 (量程 30mA ,内阻为 30Ω );
定值电阻 R 0 (阻值为 150Ω );
滑动变阻器 R (最大阻值为 100Ω );
待测电阻 R x ;
开关 S ,导线若干。
测量电路如图所示。
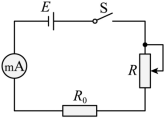
( 1 )断开开关,连接电路,将滑动变阻器 R 的滑片调到阻值最大一端。将定值电阻 R 0 接入电路;闭合开关,调节滑片位置。使电流表指针指在满刻度的 处。该同学选用的电流表为 (填 “A 1 ” 或 “A 2 ” );若不考虑电池内阻。此时滑动变阻器接入电路的电阻值应为 Ω 。
( 2 )断开开关,保持滑片的位置不变。用 R x 替换 R 0 ,闭合开关后,电流表指针指在满刻度的 处,则 R x 的测量值为 Ω 。
( 3 )本实验中未考虑电池内阻,对 R x 的测量值 (填 “ 有 ” 或 “ 无 ” )影响
A 1 60 100 无
【详解】( 1 ) [1] 若不考虑电源内阻,且在电源两端只接 R 0 时,电路中的电流约为
由题知,闭合开关,调节滑片位置,要使电流表指针指在满刻度的 处,则该同学选到的电流表应为 A 1 。
[2] 当不考虑电源内阻,根据闭合电路的欧姆定律有
计算出
R = 60Ω
( 2 ) [3] 断开开关,保持滑片的位置不变,用 R x 替换 R 0 ,闭合开关后,有
代入数据有
R x = 100Ω
( 3 ) [4] 若考虑电源内阻,根据闭合电路的欧姆定律有
联立计算出的 R x 不受电源内阻 r 的影响。
在天宫课堂中、我国航天员演示了利用牛顿第二定律测量物体质量的实验。受此启发。某同学利用气垫导轨、力传感器、无线加速度传感器、轻弹簧和待测物体等器材设计了测量物体质量的实验,如图甲所示。主要步骤如下:
① 将力传感器固定在气垫导轨左端支架上,加速度传感器固定在滑块上;
② 接通气源。放上滑块。调平气垫导轨;
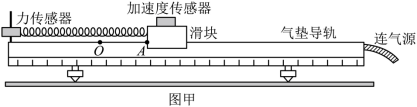
③ 将弹簧左端连接力传感器,右端连接滑块。弹簧处于原长时滑块左端位于 O 点。 A 点到 O 点的距离为 5.00cm ,拉动滑块使其左端处于 A 点,由静止释放并开始计时;
④ 计算机采集获取数据,得到滑块所受弹力 F 、加速度 a 随时间 t 变化的图像,部分图像如图乙所示。

回答以下问题(结果均保留两位有效数字):
( 1 )弹簧的劲度系数为 N/m 。
( 2 )该同学从图乙中提取某些时刻 F 与 a 的数据,画出 a — F 图像如图丙中 I 所示,由此可得滑块与加速度传感器的总质量为 kg 。
( 3 )该同学在滑块上增加待测物体,重复上述实验步骤,在图丙中画出新的 a — F 图像 Ⅱ ,则待测物体的质量为 kg 。
12 0.20 0.13
【详解】( 1 ) [1] 由题知,弹簧处于原长时滑块左端位于 O 点, A 点到 O 点的距离为 5.00cm 。拉动滑块使其左端处于 A 点,由静止释放并开始计时。结合图乙的 F — t 图有
Δ x = 5.00cm , F = 0.610N
根据胡克定律
计算出
k ≈ 12N/m
( 2 ) [2] 根据牛顿第二定律有
F = ma
则 a — F 图像的斜率为滑块与加速度传感器的总质量的倒数,根据图丙中 I ,则有
则滑块与加速度传感器的总质量为
m = 0.20kg
( 3 ) [3] 滑块上增加待测物体,同理,根据图丙中 II ,则有
则滑块、待测物体与加速度传感器的总质量为
m ′ ≈ 0.33kg
则待测物体的质量为
Δ m = m ′ - m = 0.13kg
如图所示, 平面的第一、三象限内以坐标原点 O 为圆心、半径为
的扇形区域充满方向垂直纸面向外的匀强磁场。边长为 L 的正方形金属框绕其始终在 O 点的顶点、在
平面内以角速度
顺时针匀速转动,
时刻,金属框开始进入第一象限。不考虑自感影响,关于金属框中感应电动势 E 随时间 t 变化规律的描述正确的是( )
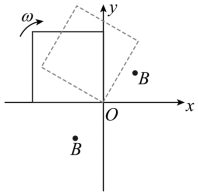
A .在 到
的过程中, E 一直增大
B .在 到
的过程中, E 先增大后减小
C .在 到
的过程中, E 的变化率一直增大
D .在 到
的过程中, E 的变化率一直减小
BC
【详解】 AB .如图所示
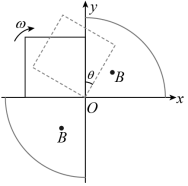
在 到
的过程中,线框的有效切割长度先变大再变小,当
时,有效切割长度最大为
,此时,感应电动势最大,所以在
到
的过程中, E 先增大后减小,故 B 正确, A 错误;
CD .在 到
的过程中,设转过的角度为
,由几何关系可得
进入磁场部分线框的面积
穿过线圈的磁通量
线圈产生的感应电动势
感应电动势的变化率
对 求二次导数得
在 到
的过程中
一直变大,所以 E 的变化率一直增大,故 C 正确, D 错误。
故选 BC 。
如图所示,某同学将离地 的网球以
的速度斜向上击出,击球点到竖直墙壁的距离
。当网球竖直分速度为零时,击中墙壁上离地高度为
的 P 点。网球与墙壁碰撞后,垂直墙面速度分量大小变为碰前的 0.75 倍。平行墙面的速度分量不变。重力加速度 g 取
,网球碰墙后的速度大小 v 和着地点到墙壁的距离 d 分别为( )
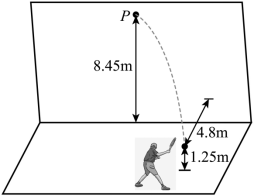
A . B .
C .
D .
BD
【详解】设网球飞出时的速度为 ,竖直方向
代入数据得
则
排球水平方向到 点的距离
根据几何关系可得打在墙面上时,垂直墙面的速度分量
平行墙面的速度分量
反弹后,垂直墙面的速度分量
则反弹后的网球速度大小为
网球落到地面的时间
着地点到墙壁的距离
故 BD 正确, AC 错误。
故选 BD 。
某同学采用图甲所示的实验装置研究光的干涉与衍射现象,狭缝 ,
的宽度可调,狭缝到屏的距离为 L 。同一单色光垂直照射狭缝,实验中分别在屏上得到了图乙,图丙所示图样。下列描述正确的是( )
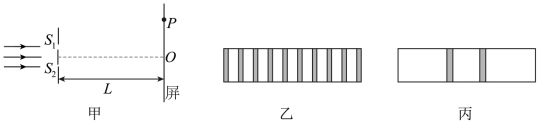
A .图乙是光的双缝干涉图样,当光通过狭缝时,也发生了衍射
B .遮住一条狭缝,另一狭缝宽度增大,其他条件不变,图丙中亮条纹宽度增大
C .照射两条狭缝时,增加 L ,其他条件不变,图乙中相邻暗条纹的中心间距增大
D .照射两条狭缝时,若光从狭缝 、
到屏上 P 点的路程差为半波长的奇数倍, P 点处一定是暗条纹
ACD
【详解】 A .由图可知,图乙中间部分等间距条纹,所以图乙是光的双缝干涉图样,当光通过狭缝时,同时也发生衍射,故 A 正确;
B .狭缝越小,衍射范围越大,衍射条纹越宽,遮住一条狭缝,另一狭缝宽度增大,则衍射现象减弱,图丙中亮条纹宽度减小,故 B 错误;
C .根据条纹间距公式 可知照射两条狭缝时,增加 L ,其他条件不变,图乙中相邻暗条纹的中心间距增大,故 C 正确;
D .照射两条狭缝时,若光从狭缝 、
到屏上 P 点的路程差为半波长的奇数倍, P 点处一定是暗条纹,故 D 正确。
故选 ACD 。
一列简谐横波沿 x 轴传播,平衡位置位于坐标原点 O 的质点振动图像如图所示。当 时,简谐波的波动图像可能正确的是( )
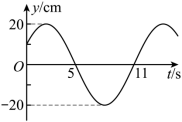
A .  B .
B . 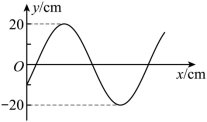
C . 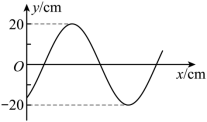 D .
D . 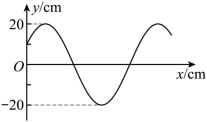
AC
【详解】由 O 点的振动图像可知,周期为 T =12s ,设原点处的质点的振动方程为
则
解得
在 t =7s 时刻
因
则在 t =7s 时刻质点在 y 轴负向向下振动,根据 “ 同侧法 ” 可判断若波向右传播,则波形为 C 所示;若波向左传播,则波形如 A 所示。
故选 AC 。
查看答案